When it comes to measuring the value of things on Mars, it’s hard to find a baseline. You can balance things against import mass (like the slugs of Andy Weir’s Artemis), or the raw dollar cost considering launch and purchase cost. Both start to fall apart as our settlement industrialises and the value of goods is tied more and more to Mars rather than Earth. Enter a new value basis – one with a fixed root in engineering that can scale to any settlement beyond Earth. Enter the hydrogen economy.
Anyone who’s studied engineering thermodynamics at undergraduate level is probably familiar with the concept of exergy. If you haven’t, it’s simple – exergy is a measure of the vague “potential of a system to do work”. Once you account for unavoidable entropic losses, the exergy change of a process is the maximum possible energy that can be extracted from it. It’s also noteworthy because it’s a totally physically meaningless metric but still manages to provide a lot of useful insight into the engineering of a system. Exergy isn’t relevant to the rest of this piece but I think it’s a nice analogy for a meaningless, very useful analysis method.
Value in Space
Three things are valuable in space, all because they’re in short supply. Energy (you only have so many solar panels and so many hours of sunlight), mass and money. All three of them can be swapped around and converted into each other – energy requires mass in the power system, mass requires money to pay for the rocket – but that conversion can often carry lots of assumptions. Comparing across analyses it quickly becomes impossible to square the different numbers chosen by different analysts, often in different decades. This is made more complicated by the fact that each of those three drivers – energy, mass and cost – have different values in different contexts. Energy is far more valuable at Jupiter, where the sunlight is weak, than it is at Mercury. Mass is more valuable in orbit than on the surface of a planet. The complexity explodes very rapidly.
So, we need a unified metric to determine the value of things. It should have some kind of normalisation for different situations. It should encompass the measurement of as many valuable things as possible. And ideally it should be easy to understand. Well, that last one is tricky. But I do my best.
As a comparator – the value against which all other values are measured – you can certainly do a lot worse than hydrogen. Space settlements will need a lot of it – it’s the basis for almost every propellant production, a byproduct of oxygen generation and the feedstock for chemical engineering. So, to determine the value of a process or material, consider the three inputs (energy, mass and cost) that went into making them and bringing them to Mars. Ask, if we’d instead invested those resources into just making more hydrogen, how many kilograms of hydrogen would we have? And that’s the value of the process or material in Hy! It’s that simple!
Well, of course it isn’t. The value of the Hy, referred back to energy or mass or dollars, isn’t a constant. It varies with the industrial base of the settlement it’s made in. But this is a good thing! We want to understand the value of things in the context in which they’re made.
Hydrogen on Mars
For starters, lets’ work out the value of the Hy at two points in time. Firstly, the minute after the first landing on Mars. The only way to get hydrogen is to buy it on Earth and import it. At this point, the value of hydrogen is pretty much the same as the value of any other material.
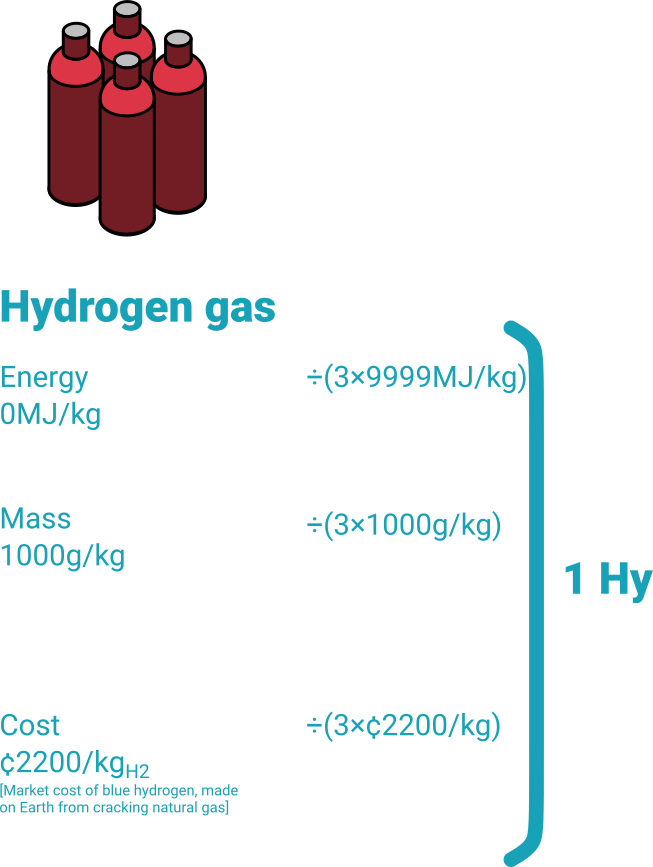
But we won’t import hydrogen forever – in order to sustainably refuel vehicles, we have to make it in-situ. So once we use Rodwells and electrolysis to generate our hydrogen, the value looks like this instead:
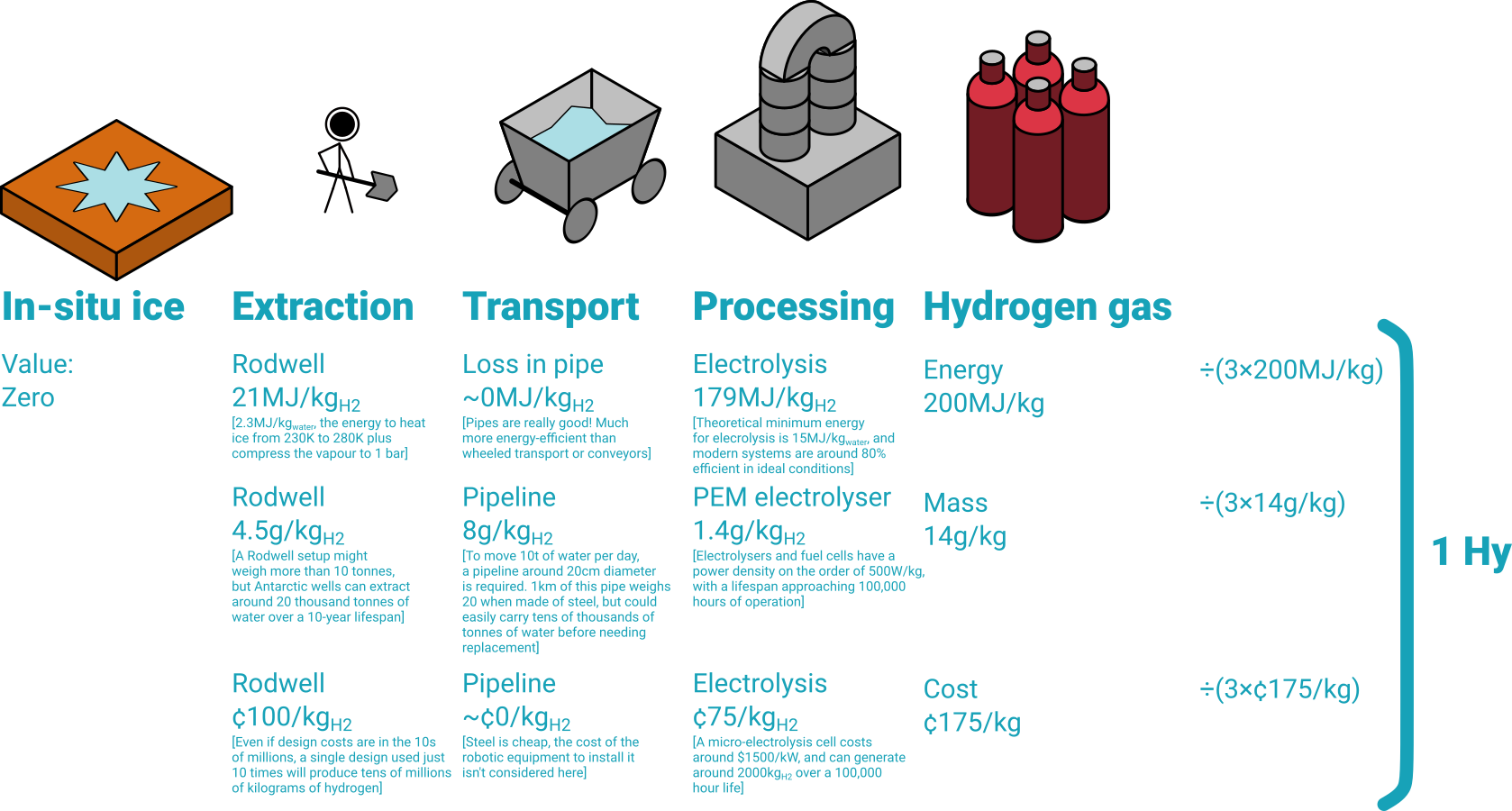
That’s a pretty radical difference! Suddenly we care about energy, because it’s in a limited supply on Mars. But we aren’t trying to estimate solar panel masses or lifetimes to estimate the dollar value of anything. All the mathematics is out in the open. 1 Note: there is one, and just one, bit of handwavey mathematics in this. Notice that in the normalisation, I divided by 3 to have 1 kg of hydrogen cost 1 Hy? That’s a choice and it’s an arbitrary one. Depending on the situation, and particularly depending on the location, you can choose different coefficients as long as they sum to 1 appropriately. A settlement at Jupiter might put much more focus on energy and mass, and less on cost, because that’s what is valuable at Jupiter. However you can still use a short definition of the Hy vector, by incorporating the multiplier into the value. In this case, the first Hy is defined as [29997, 3000, 6900] and the second is [600, 42, 525]. Equally neat, but it’s complicating an already long piece so it’s banished to the footnote. You can define the entire industrial “context” of the Hy with three numbers. In the first case, we were using a just-landed Hy of [9999, 1000, 2300]. In the second, the Hy is defined as [200, 14, 175]. The notation is simple, unambiguous and looks enough like a vector to make my engineer brain happy.
The value of a moment
So now we have the definition, let’s evaluate! Likely the fourth-most valuable thing in a space settlement is crew time. I considered actually including it as a fourth input to the Hy, but it got sprawling and over complicated very quickly. So instead lets evaluate how much crew time is actually worth. We’re using the [200, 14, 175] Hy definition, and growing food for the crew on Mars using artificially lit hydroponics.
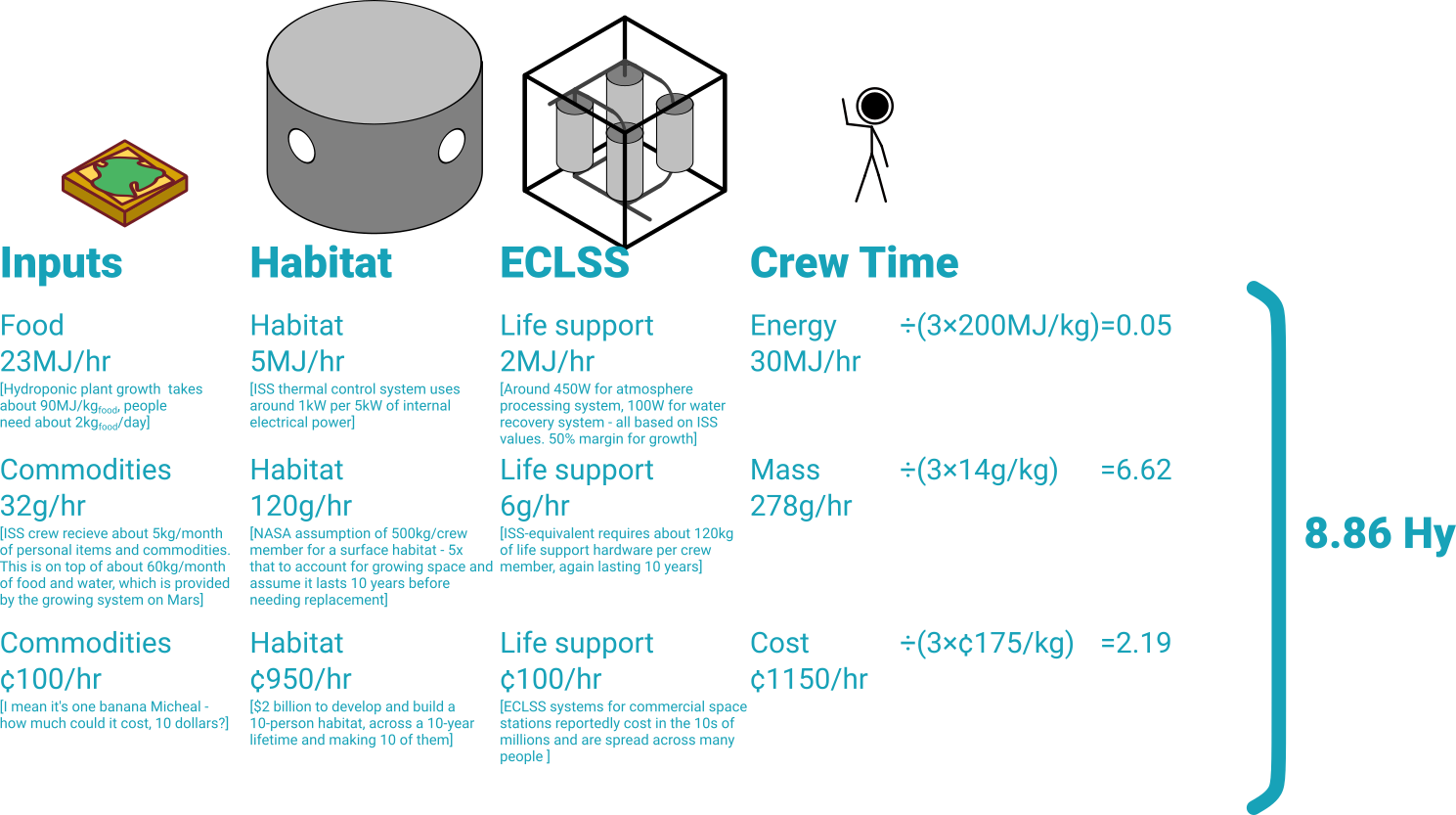
That looks … reasonable? I think? 8.9kg of hydrogen per hour of crew time is a lot – the buoyancy is enough to lift a person. This also shows where the “cost” of crew comes from – almost entirely in the habitat, and the majority of that from the volume needed to grow food. It’s worth noting that if we didn’t grow any food, the cost of the crew-hour comes out around 11 Hy – the import mass is really that valuable. There is probably some intermediate minimum point but we’re not here to find that. By converting the entire Hy value to dollars, you eventually pop out a number in the ballpark of $35,000 per hour 2 Assuming Starship initially launches at $800/kg, and launching pressurised cargo is 20x as expensive – the same multiplier between Falcon 9 and Cargo Dragon. Plus another 10x multipler for deep-space operations which pays for the mission control, you end up with a cost of about $100,000/kg to the surface of Mars. The mass cost of the power can be estimated from NASA’s Life Support BVAD document, and comes out to be about about 200kg/kW, or 1000kg of solar panel needed to support our 5-tonne habitat and growing system. The cost per hour of that system, with a 10-year lifespan, is just 80g/hr. We don’t need to add in the solar panel purchase costs of $500/W, or $2/hr – they’re basically negligble. Overall, we have about 350g per hour, or $35,000. BVAD lists a first-guess estimate of 0.45kg/hr and we’re definitely making a saving by growing food locally, so that’s a very neat final check on the numbers. – given that NASA currently charges commercial users $150,000 per hour of astronaut time and the ISS was built with much more expensive launchers than Starship, I’m happy that this value makes sense.
The nuts and bolts of the question
We can also work out the cost of other materials, including those with inputs and intermediates that already have values defined in Hy. A very pertinent one for Mars is steelmaking – hydrogen is used as a reducing agent, but very substantial amounts of energy are also used for melting in the electric arc furnace and in the rolling mills. We might expect the calculation to be energy-dominated, especially once the “embodied energy” of hydrogen is considered.
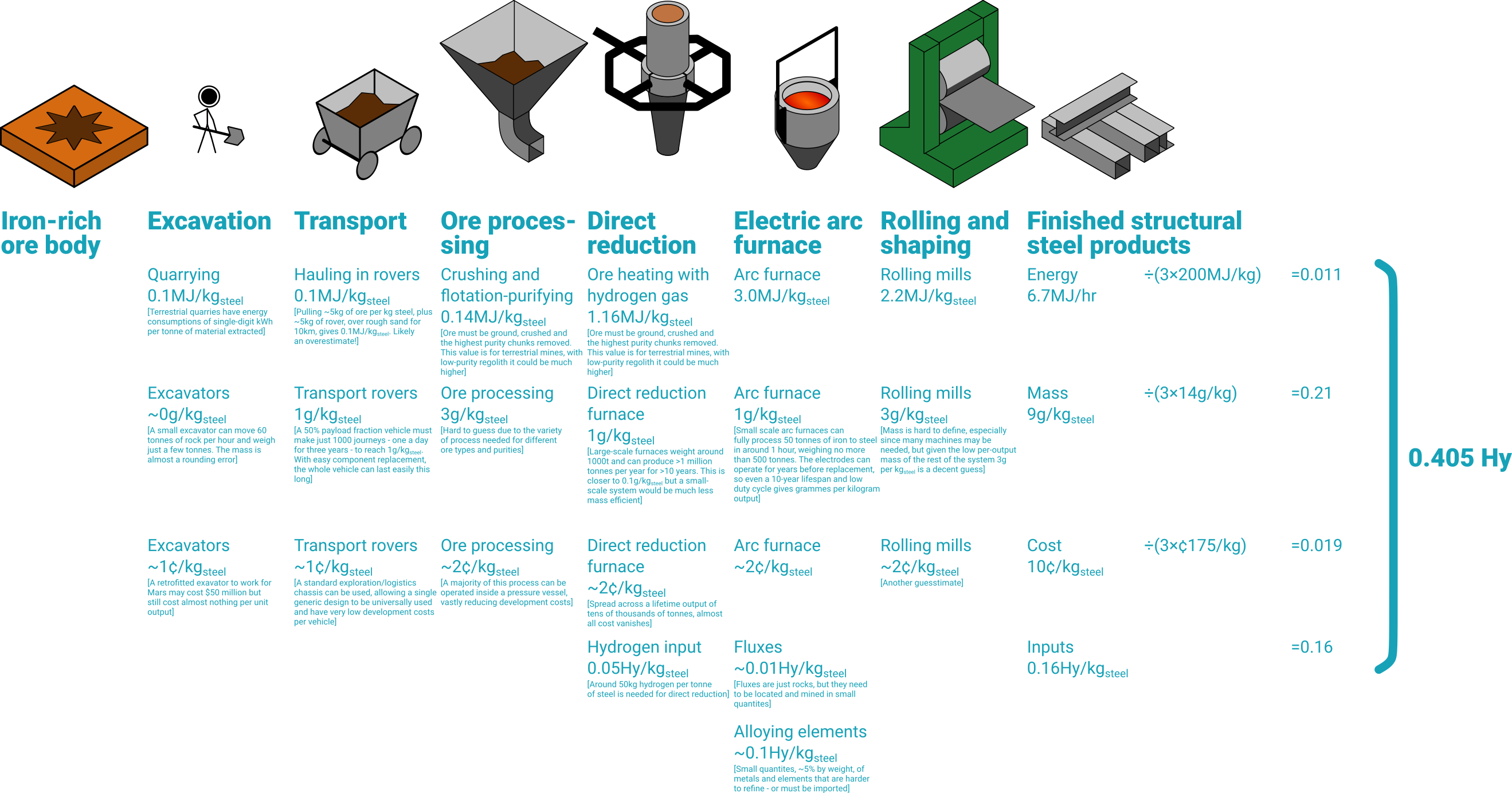
Not what we thought! It turns out both the energy and hydrogen addition are very small parts of the total cost balance of the steel. What sinks us is the mass and cost of the machinery – even if it lasts years and produces tens of thousands of tonnes, this stuff is expensive and very heavy. It’s also not a trivial problem to commission this ISRU chain. It sounds obvious but a steel mill is mostly made of steel, which can’t be made without a steel mill. Either we pay the mass to import the whole thing in one go, or spend a lot of money on Earth designing successively smaller von Neumann steel mills. With this analysis, it would be possible to determine which is better! Another unexpected cost point is the alloying elements. I assumed they were 5 times more costly than steel and we used 5%wt – not necessarily the case for every element and every steel!
Choo Choo
So finally, we want to show off how this whacky system – converting all our equipment costs to hydrogen and back again, to analyse two options end-to-end. Let’s re-examine our steel mill. The production is very cheap and (we think) scales well, as much of the equipment can be run with long lives and relatively high duty cycles. We want to deliver more iron-rich ore – much, much more ore – to the system, which requires a high-throughput line about 10km long. The options are clearing a road and using the same general-purpose rovers as the rest of the settlement to haul trailers, or lay an honest-to-god railroad. This analysis has a lot more assumptions3Assumptions: All vehicles are good for 10,000 journeys before replacement. Unloading wagons/carts takes 10 minutes per wagon. The numbers for import/ISRU mass are chosen because they “look about right”, not based on anything rigorous. Speeds and transit times calculated assuming a flat track. Lifetime throughput of the locomotive is 3 million tonnes, versus 1.4 million tonnes for the rovers., because I’m not willing to do a complete trade study to prove a point here.
For the rovers, the higher friction on a compacted sand road means you can pull much less – about 30 times less – with the same tractive effort as the train, and you’re limited to a lower top speed. Overall the throughput of a gang of rovers is about 3kg/s during operation – a whole 14 times less than the rails! So we need 14 rovers working in parallel to match the system capabilities. This is a clear deficiency in the analysis – almost all the cost of upgrading the rover’s throughput is marginal, so it’s much easier to spool up and down. In comparison, the high capital cost of building the rail line makes it costly to run the train at much less than 100% capacity.

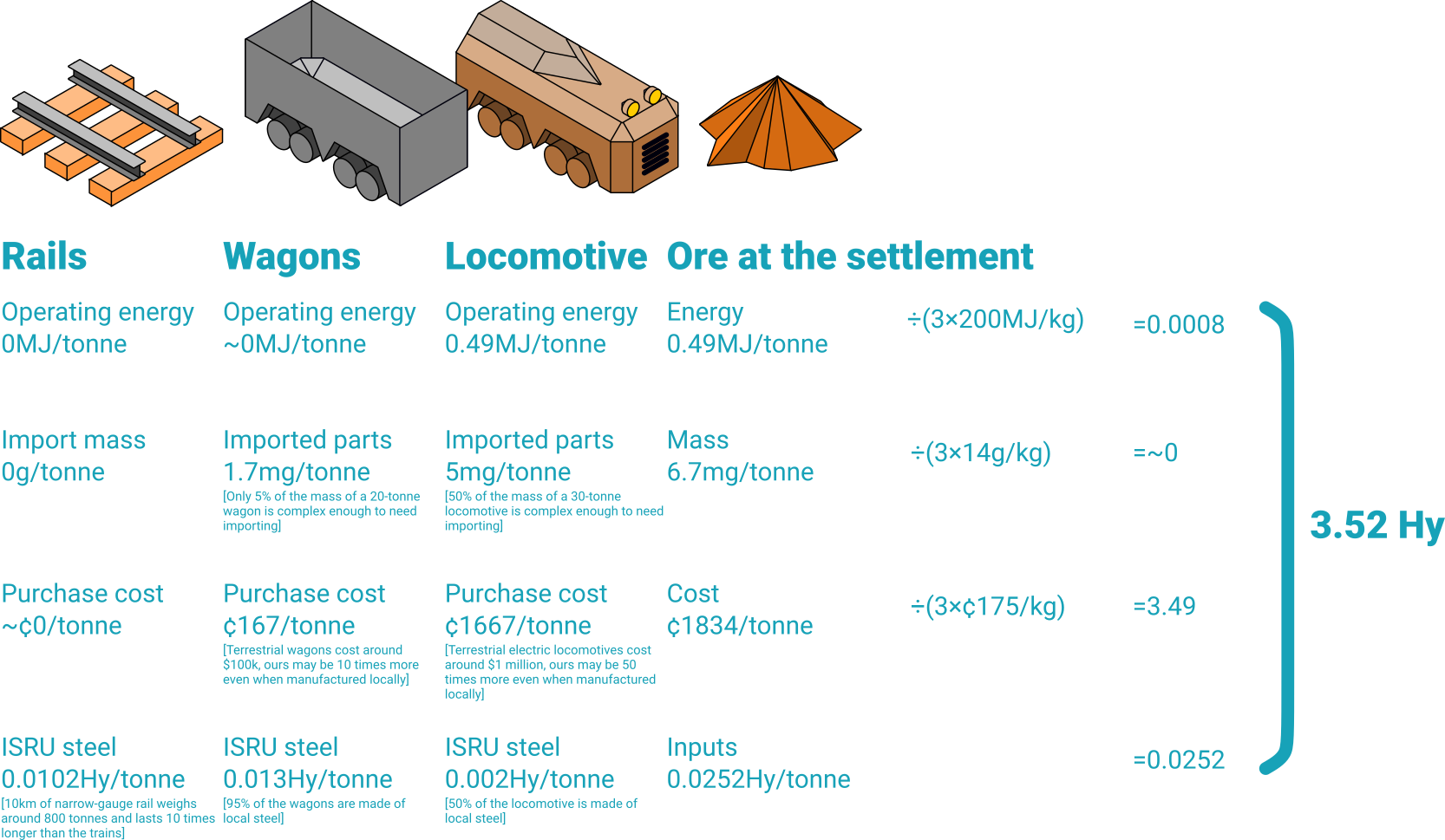
Nice! This reveals some interesting insights about both systems, and helps us make a clear choice. As we expected, the power consumption of the rail is substantially lower than the rovers, at the expense of more locally-produced steel. The difference in the latter is less than we might have expected – largely because the enormous 300,000Hy cost of the rails is spread across 30 million tonnes – or more than 10 years – of operation. The import mass of the rovers actually winds up higher, because we need to import many separate drive and power systems rather than one big one. But unexpectedly, all other costs are dwarfed by the design and purchase costs of the hardware. The values I’ve chosen are only ~10 times more expensive than extremely well-tested terrestrial systems, so this really proves the enormous benefit that could be won if one could retrofit existing hardware for Mars rather than designing from scratch.
The last insight that can be worked out is the initial investment that must be made to bring the systems operational. This is very simple to find – just multiply the relevant costs by the lifetime throughput. For the trains, we must invest about 10.8 million Hy – 97% in the purchase of the locomotive and wagons. For the rovers the investment is only 8.1 million Hy – indicative of the lower lifetime throughput of the system.
Lessons from Hydrogen
Climbing back out of the rabbithole, what does this methodology allow for? It’s a way to normalise the cost – technical and financial – of building in space, and providing a fair baseline for comparing between different systems. Converting from a multi-factor analysis to Hy doesn’t require much additional work and reveals a great deal about both the relative merit of two systems, and the breakdown of where the costs of a system are generated. In short this is an approach I really like, and it’ll certainly be returning in future articles. Like so much of engineering analysis, looking at the same problem through a new lens can provide the insight that counts. For the economics of Mars, that lens might be unexpectedly rich in hydrogen.
